Polynomial Equations
A polynomial function $p(x)$ is not an equation. An equation implies equality, preferably to zero and must contain an $=$ sign.
Linear Equations
\[ ax+b=0 \qquad a \neq 0 \]
\[ x = {-b\over a} \]
Quadratic Equations
\[ ax^2+bx+c=0 \]
There are three main methods to solve quadratic equations.
- factorising (always try this first)
- using 'the formula'
- completing the square
Factorisation
To solve $x^2-4x-21=0$:
$(x+3)(x-7)=0 \quad \Rightarrow \quad x=-3, \ \mbox{or}\ x = 7$
Formula
$\displaystyle x=\displaystyle \frac{-b\pm \sqrt {b^2-4ac}}{2a}$
$b^2-4ac$ is called the discriminant.
- If the descriminant is zero then there is one real solution, sometimes referred to as two equal solutions.
- If it is greater than zero, there are two different (distinct) real solutions.
- If it is less than zero, there are no real solutions, but two complex conjugate solutions. (A number is complex if it contains $\sqrt -1$, represented by $i$ or $j$)
Completing the square
To solve
\[ \begin{array}{lrcl}& x^{2} - 4x + 3 & =& 0\\ \Rightarrow & (x - 2)^{2} - 4 + 3& =& 0\\ \Rightarrow & (x - 2)^{2}& =& 1\\ \Rightarrow & x - 2& =& \pm \sqrt {1}\\ \Rightarrow & x& =& 2\pm \sqrt {1}\\ \Rightarrow & x& =& 3 \hbox{ or } 1\\ \end{array} \]
Note: In this case the quadratic expression would factorise and it would have been easier to factorise than to complete the square.
Quadratic Graphs
$y=ax^2+bx+c$
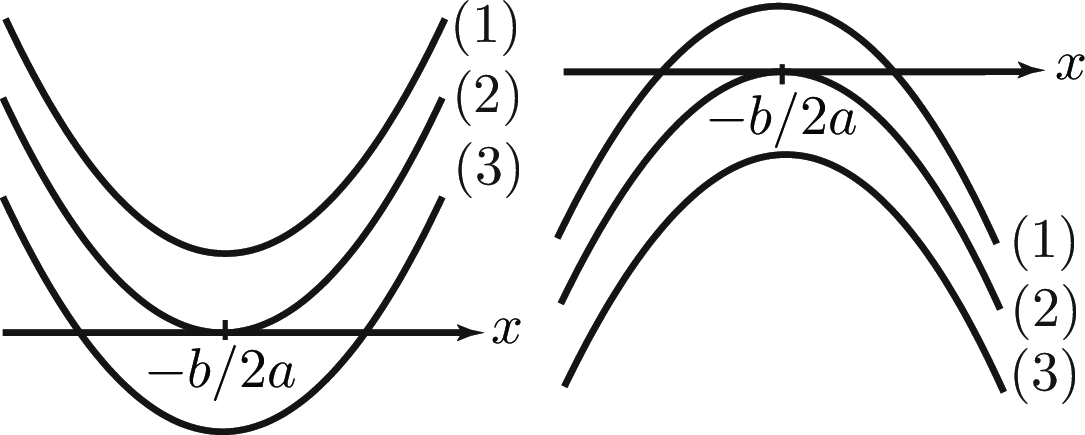
\[ \matrix { & a>0 & & & a<0 & \qquad \cr (1) & b^2-4ac<0 & \qquad & (1) & b^2-4ac>0& \cr (2) & b^2-4ac=0 & & (2) & b^2-4ac=0& \cr (3) & b^2-4ac>0 & & (3) & b^2-4ac<0& \cr } \]
To help sketch graphs the process of completing the square can be very useful.
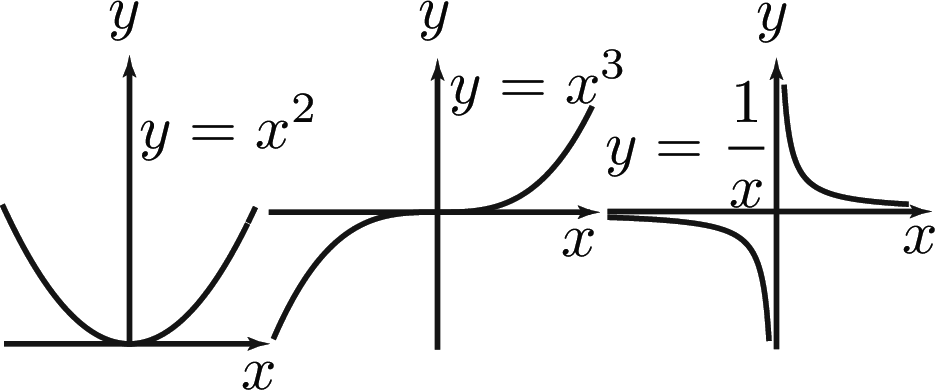
Graphs of other common functions
Graphs of $y=x^2$, $y=x^3$ and $\displaystyle y=\frac{1}{x}, \ y=a^ x\ (a>1)$
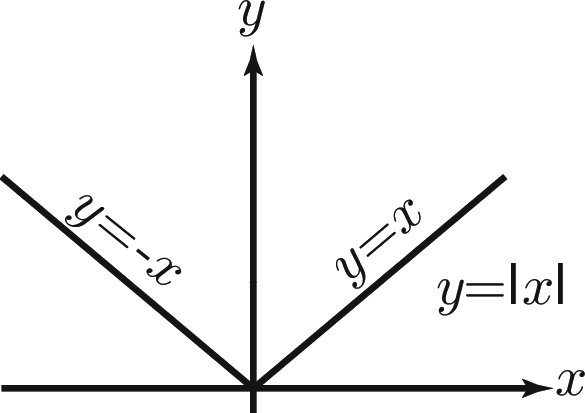
The modulus function
\[ |x| = \left\{ \matrix {x & {\rm if } & x\geqslant 0 \cr -x & {\rm if } & x<0\cr }\right. \]
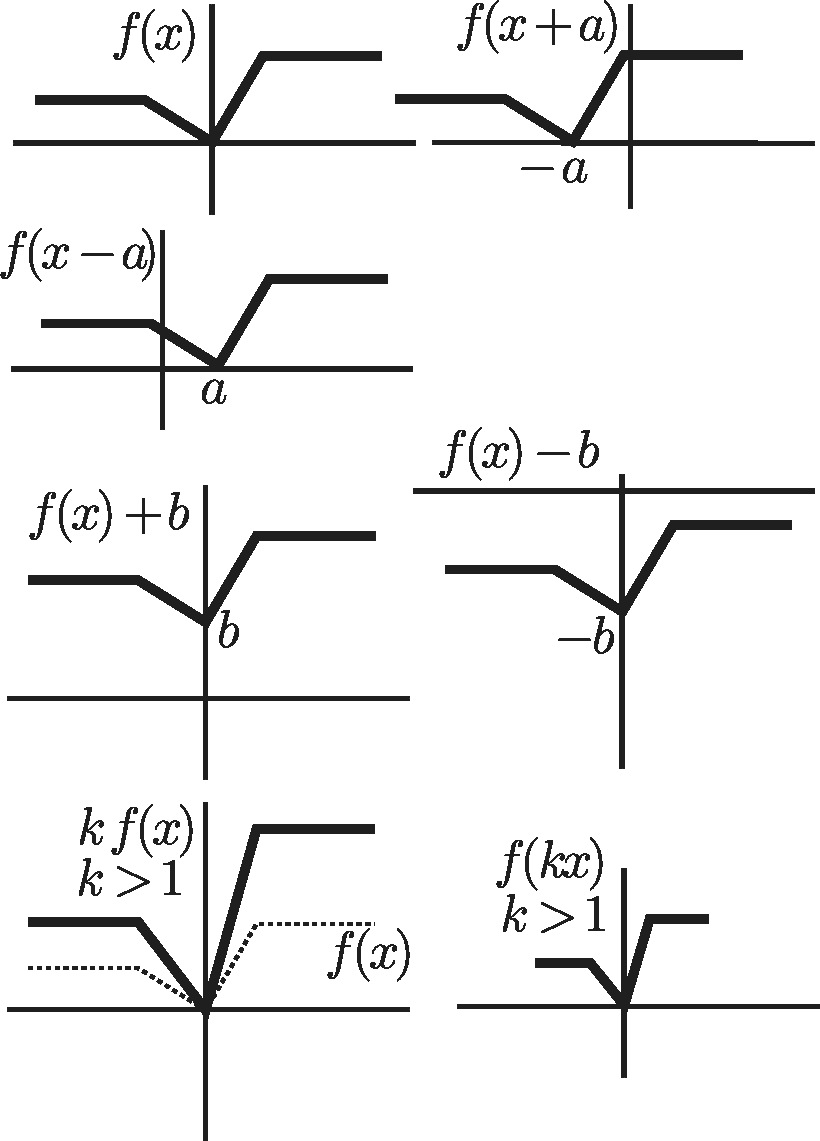
Basic Transformations
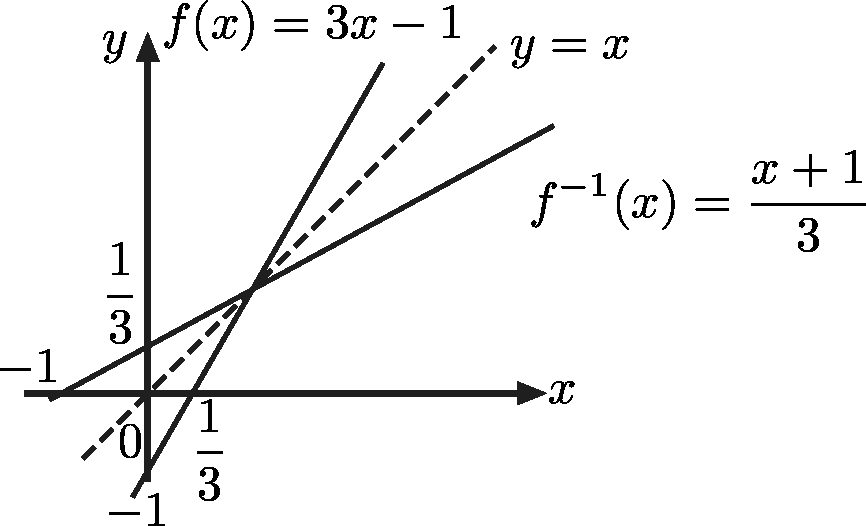
Graphs of Inverse Functions
The graphs of a function and its inverse have reflection symmetry about the line $y = x$
Example: consider the function $f(x)=3x-1$
Its inverse is $f^{-1}(x)=\displaystyle \frac{x+1}{3}$
These can be shown graphically as
Polynomials
A polynomial function, $p(x)$, is made by summing terms which contain only positive integer powers of x together, perhaps with a constant.
Note: The polynomial may contain just one term.
Examples
$2x^{3}+5x, \quad 3x+2 ,\quad 7 $
In general,
$p\left(x\right) = a_{0}+a_{1}x+a_{2}x^{2}+\ldots +a_{n}x^{n} = \displaystyle \sum _{i=0}^{n}a_{i}x^{i}$
$a_{i}$ are the coefficients of $x^{i}$ and may be zero.
($a_{0}x^{0}=a_{0}$ since $x^{0}=1$ and $a_{1}x^{1}=a_{1}x$ since $x^{1}=x$)
Degree of a polynomial
The degree of a polynomial is the value of the highest power of $x$.
A polynomial of degree 1 is called linear, one of degree 2 is quadratic, one of degree 3 is cubic and one of degree 4 is quartic.
Factorisation & Expansion
Factorisation
Difference of two squares:
\[ x^2-a^2= (x-a)(x+a) \]
Difference of two cubes:
\[ x^3-a^3=(x-a)(x^2+ax+a^2) \]
Sum of two cubes:
\[ x^3+a^3=(x+a)(x^2-ax+a^2) \]
Expansions
\[ \begin{array}{rcl} (x+a)^2& =& x^2+2ax+a^2 \\ (x-a)^2& =& x^2-2ax+a^2 \\ (x+a)^3& =& x^3+3ax^2+3a^2x+a^3 \\ (x-a)^3& =& x^3-3ax^2+3a^2x-a^3 \end{array} \]
The Factor Theorem
For a given polynomial $p(x)$, if $p(a) = 0$ then $(x - a)$ is a factor of $p(x)$.
Following on from this, if $(x - a)$ is a factor of $p(x)$ then $p(a) = 0$.
The Remainder Theorem
If a polynomial $p(x)$ is divided by $(x - a)$, the remainder is $p(a)$.
Partial Fractions
For proper fractions $\displaystyle {P(x)\over Q(x)}$ where $P$ and $Q$ are polynomials with the degree of $P$ less than the degree of $Q$:
a linear factor $ax+b$ in the denominator produces a partial fraction of the form $\displaystyle {A\over ax+b}$
repeated linear factors $\displaystyle (ax+b)^2$ in the denominator produce partial fractions of the form $\displaystyle {A\over ax+b}+\displaystyle {B\over (ax+b)^2}$
a quadratic factor $ax^2+bx+c$ in the denominator produces a partial fraction of the form $\displaystyle {Ax+B\over ax^2+bx+c}$
Improper fractions require an additional term. This is a polynomial of degree $n-d$ where $n$ is the degree of the numerator and $d$ is the degree of the denominator.
Inequalities
\[ a>b \hbox{ means } a \hbox{ is greater than } b \]
\[ a<b \hbox{ means } a \hbox{ is less than } b \]
\[ a\geqslant b \hbox{ means } a \hbox{ is greater than or equal to } b \]
\[ a\leqslant b \hbox{ means } a \hbox{ is less than or equal to } b \]
\[ |x|<k \hbox{ means } -k<x<k \]
\[ |x|>k \hbox{ means } x>k \hbox{ or } x<-k \]
The Binomial Theorem
Pascal's triangle
\[ \matrix {& & & & & & 1& & & & & & \cr & & & & & 1& & 1& & & & & \cr & & & & 1& & 2& & 1& & & \cr & & & 1& & 3& & 3& & 1& \cr & & 1& & 4& & 6& & 4& & 1\cr & 1& & 5& & 10& & 10& & 5& & 1\cr \vdots & & \vdots & & \vdots & & \vdots & & \vdots & & \vdots & & \vdots \cr } \]
Note that the rows of Pascal's triangle give the coefficients in the expansion of $(a+b)^ n$:
$(a+b)^0=1$
$(a+b)^1= 1a+1b$
$(a+b)^2 = 1a^2+2ab + 1b^2$
$(a+b)^3=1a^3+3a^2b+3ab^2+1b^3$
$\vdots $
Combinations
The number of ways of making a selection of $r$ objects from a set of $n$ different objects when the order of selection is not important (e.g. selecting 6 numbers on a lottery ticket) is denoted $^ nC_ r$ or $({n\atop r})$, given by
\[ ^ nC_ r = \displaystyle \frac{n!}{r!(n-r)!}\quad \hbox{sometimes written as} \left({n\atop r}\right) \]
Factorials
$n!=n\times (n-1)\times (n-2)\times \ldots \times 3\times 2\times 1$
Here, $n$ is a positive integer. $0!$ is defined as 1.
Binomial Theorem
If $n$ is a positive integer
\[ \begin{array}{rcl} (a+b)^ n & =& a^ n + \left({n\atop 1}\right)a^{n-1}b^1+\left({n \atop 2}\right)a^{n-2}b^2 \\ & & \kern -30pt{+\ldots + \left(n\atop r\right)a^{n-r}b^ r + \ldots + b^ n \ (n\in \mathbb N)}\\ \end{array} \]
Binomial Series
If $n$ is not a positive integer
\[ \begin{array}{rcl} (1+x)^ n& =& 1+nx + {n(n-1)\over 1\times 2}x^2\\ & & +\ldots + {n(n-1)\ldots (n-r+1)x^ r\over 1\times 2\times 3 \ldots \times r}\\ & & +\ldots \end{array} \]
which is valid for any real number $n$ providing that $|x|<1$.
Indices, Exponentials & Logarithms
Laws of Indices
\[ a^ ma^ n=a^{m+n} ,\quad {a^ m\over a^ n}=a^{m-n}, \quad (a^ m)^ n=a^{mn} \]
\[ a^0=1,\ a^{-m}={1\over a^ m},\ a^{1/n}=\sqrt [n]{a}, a^{m\over n}=(\sqrt [n]{a})^ m \]
Laws of Logarithms
For any positive base $b$ (with $b\ne 1$)
\[ \log _ bA=c \quad \hbox{ means }\quad A=b^ c \]
\[ \log _ b A + \log _ b B = \log _ b AB \]
\[ \log _ b A-\log _ b B=\log _ b{A\over B}, \]
\[ n\, \log _ b A=\log _ b A^ n,\quad \log _ b 1=0, \quad \log _ bb=1 \]
Formula for change of base
$\log _ ax={\log _ bx\over \log _ b a} $
Logarithms to base e, denoted $\log _{\rm e}$ or alternatively $\ln $ are called natural logarithms. The letter e stands for the exponential constant which is approximately 2.718.
Solving equations with an unknown power
To solve $a^ x=b$ where $a>0$, $b>0$:
\begin{eqnarray*} & a^ x=b \\ \hbox{where} & a>0 \\ \hbox{and} & b>0 \\ \end{eqnarray*}
Take logs of both sides to give
\begin{eqnarray*} \log (a^ x) & =& \log b \\ x\log a & =& \log b \\ x & =& \displaystyle \frac{\log b}{\log a} \end{eqnarray*}
Logs of any base may be used including base 10 ($\log $) and base e ($\ln $).
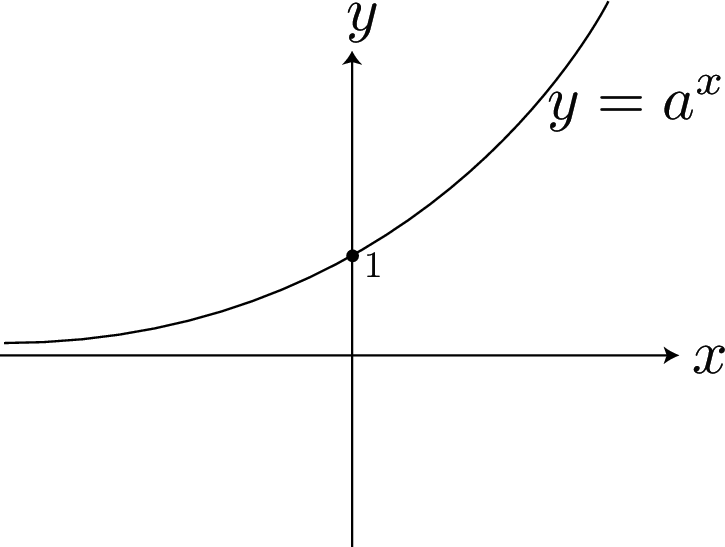
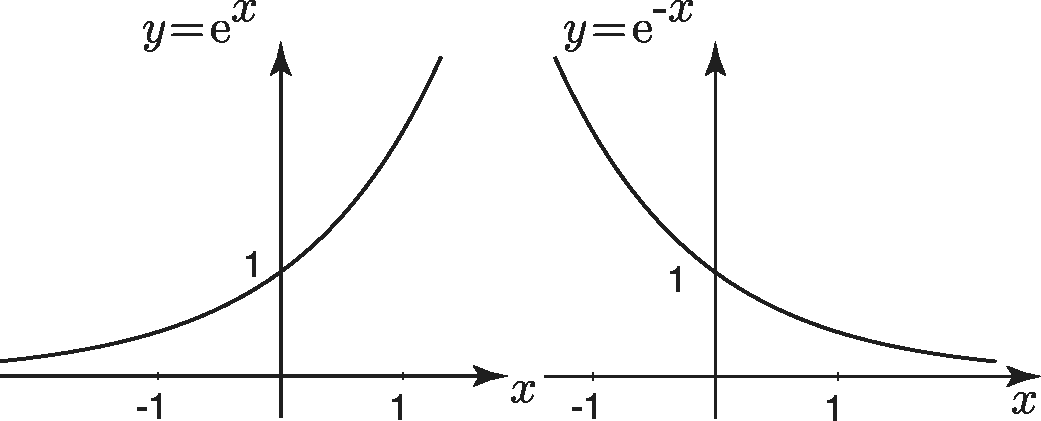
Exponential functions
A pair of graphs showing exponential growth and decay, respectively:
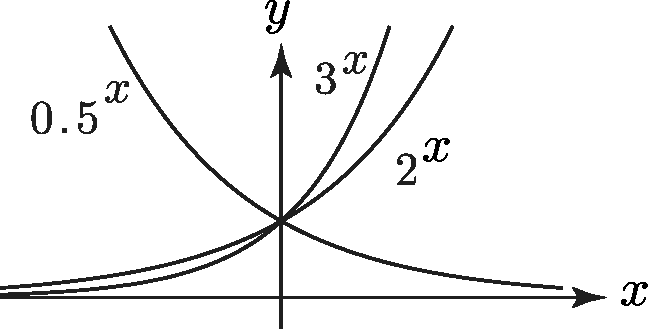
A graph of powers of different bases:
Logarithmic functions
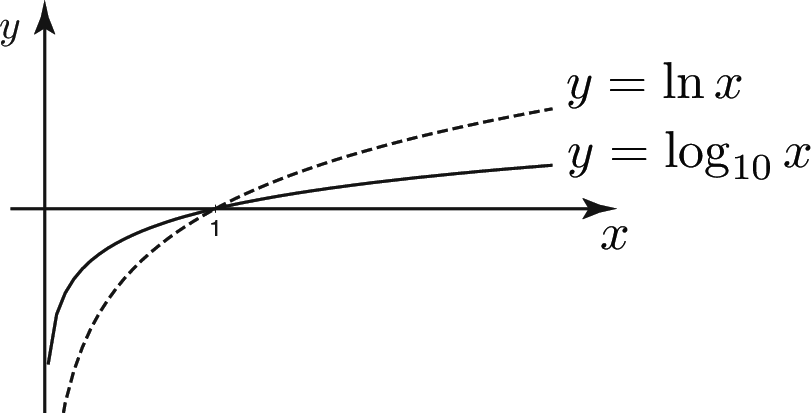
Graphs of $y=\ln x$ and $y=\log _{10} x$
\[ y=e^ x\Leftrightarrow x=\ln y \]
