Differentiation
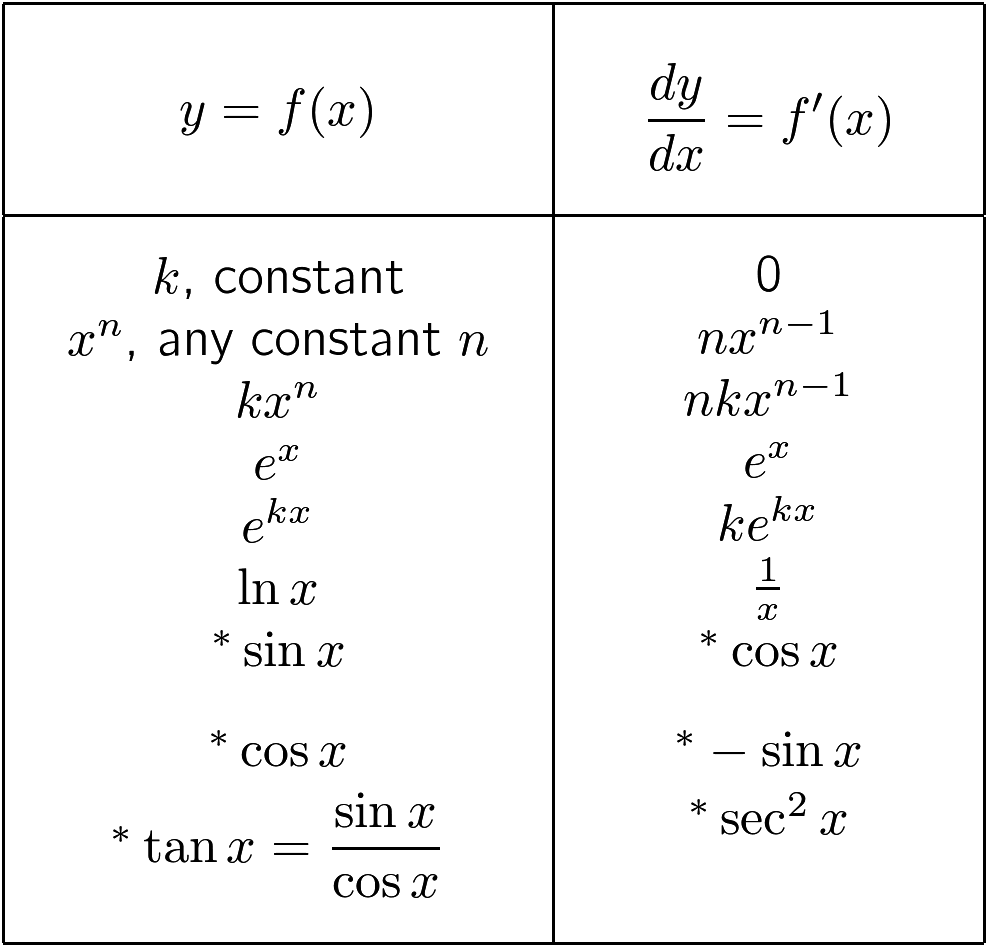
* $x$ is measured in radians.
Differentiating a Function of a Function
This can be done using the chain rule
\[ \displaystyle \frac{dy}{dx}=\displaystyle \frac{dy}{du}\times \displaystyle \frac{du}{dx} \]
The Product Rule
If $y=uv$ where $u$ and $v$ are functions of $x$
Then $\displaystyle \frac{dy}{dx}=u\displaystyle \frac{dv}{dx}+v\displaystyle \frac{du}{dx}$
The rule can be stated in function notation:
If $y=f(x)g(x)$ then $\displaystyle \frac{dy}{dx}=f(x)g’(x)+f’(x)g(x)$
The Quotient Rule
If $y=\displaystyle \frac{u}{v}$ where $u$ and $v$ are functions of $x$, then $\displaystyle \frac{dy}{dx}=\displaystyle \frac{v\displaystyle \frac{du}{dx}-u\displaystyle \frac{dv}{dx}}{v^2}$
In function notation, the derivative of $\displaystyle \frac{f(x)}{g(x)}$ is $\displaystyle \frac{f'(x)g(x)-f(x)g'(x)}{\left[ {g(x)} \right]^2}$
Differentiation of Functions Defined Parametrically
If $y=f(t)$ and $x = g(t)$ then $\displaystyle {dy\over dx} = \displaystyle {dy\over dt} \div {dx\over dt}$
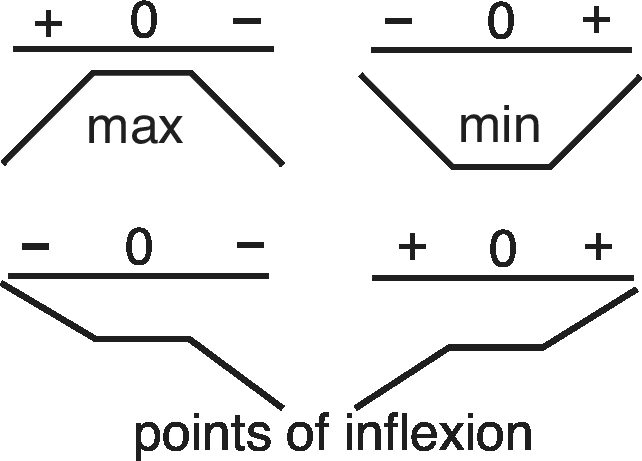
Stationary Points
A stationary point of $y=f(x)$ occurs when$\displaystyle \frac{dy}{dx}=f’(x)=0$. It may be classified as a local maximum, a local minimum, or a point of inflexion. A test using $\displaystyle \frac{d^2y}{dx^2}=f”(x)$ can be used to find the nature of the stationary point.
When $f’(a)=0$:
$f”(a)<0 \quad \rightarrow \quad $ maximum
$f”(a)>0 \quad \rightarrow \quad $ minimum
$f”(a)=0 \quad \rightarrow \quad $ needs further investigation by examining the gradient pattern either side of the point.
Integration
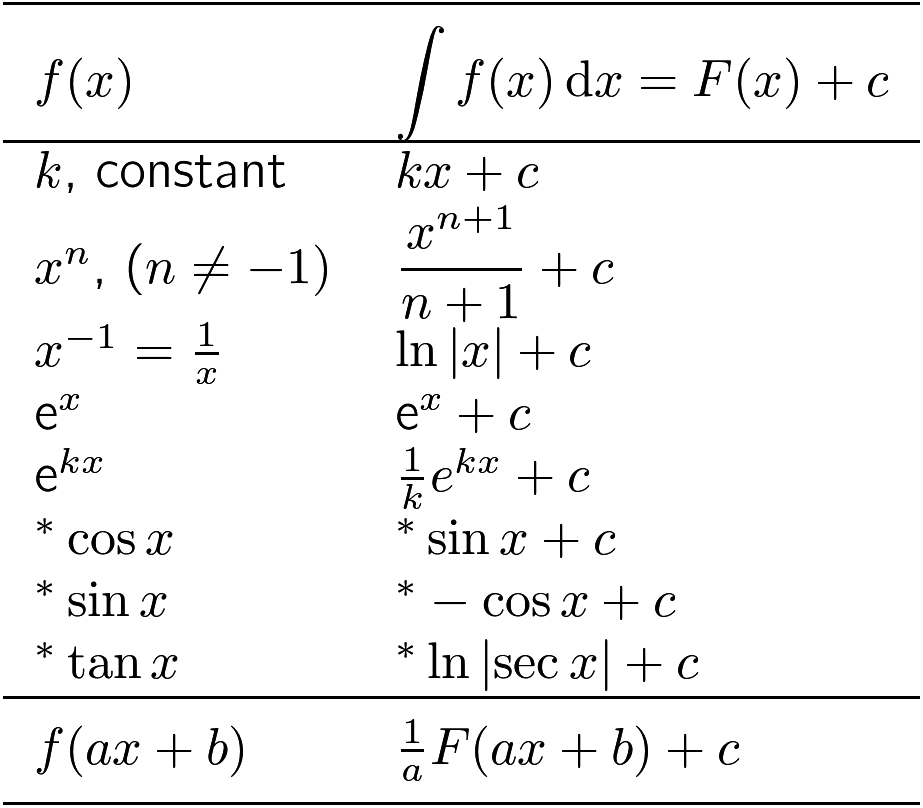
* $x$ is measured in radians.
The linearity rule for integration
$\displaystyle \int \left(af(x)+bg(x)\right){\rm d}x = $
$\displaystyle a\int \! \! f(x)\, {\rm d}x \, +\, b\displaystyle \int \! \! g(x)\, {\rm d}x, \ (a,b \, \, {\rm constant})$
Integration by parts
\[ \int _ a^ b u{{\rm d}v\over {\rm d}x}{\rm d}x=\left[uv\right]_ a^ b- \int _ a^ b v{{\rm d}u\over {\rm d}x}{\rm d}x \]
Indefinite Integrals
$\displaystyle \int x^{2}dx = \displaystyle \frac{x^{3}}{3}+c$
This contains an arbitrary constant $c$ so the integral does not have a unique value. It is called an indefinite integral.
Area under a graph
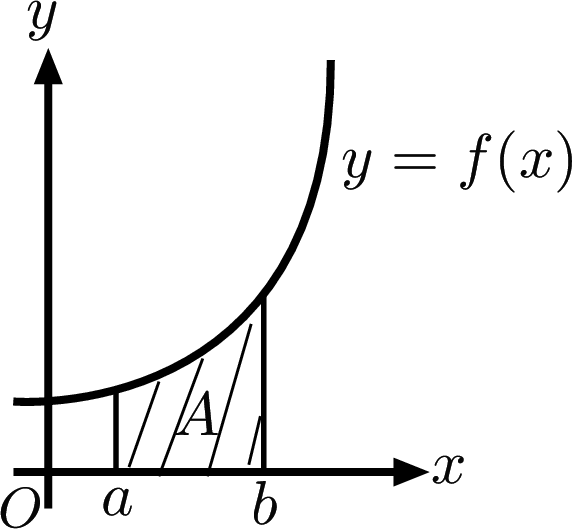
The area $A$ is bounded by the lines $x = a$ and $x = b$ and the curve $y = f(x)$. Here, $A=\int ^ b_ a f(x) dx$, $x = a$ and $x = b$ are called the lower and upper limits of the integral.
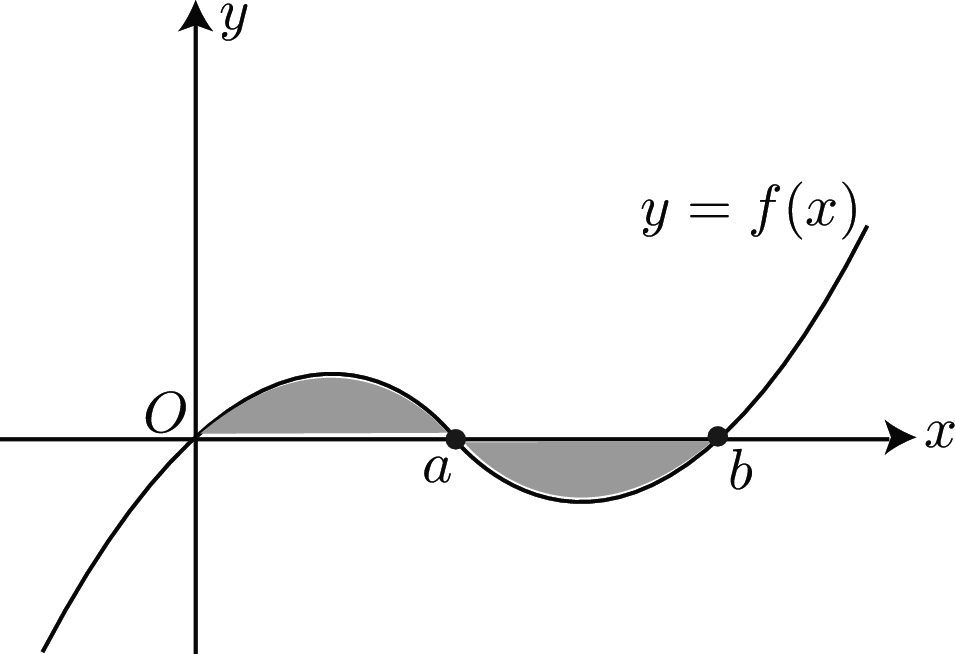
To find the shaded area enclosed between the curve $y=f(x)$ and the $x$ axis use
\[ A = \int ^ a_0f(x) dx + \left|\int ^ b_ a f(x) dx\right| \]
Volumes of revolution
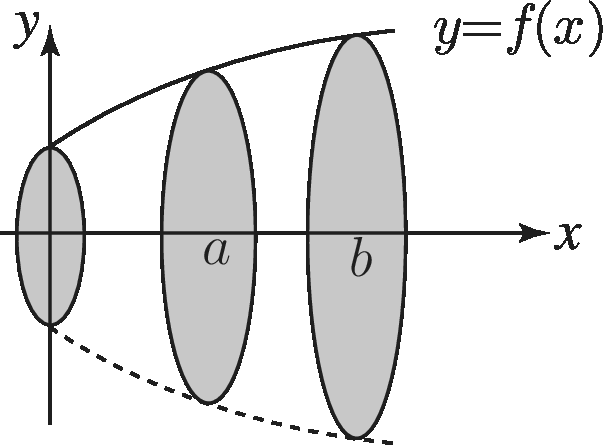
When the curve $y=f(x)$ is rotated through $2\pi $ radians about the $x$ axis the volume contained between $x=a$ and $x=b$ is found from
$\displaystyle V=\int _ a^ b\pi (f(x))^2{\rm d}x =\int _ a^ b\pi y^2{\rm d}x$.
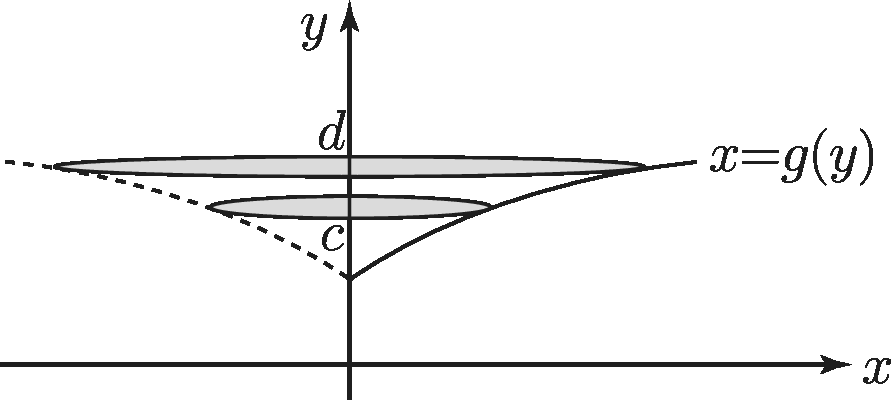
When the curve $x=g(y)$ is rotated through $2\pi $ radians about the $y$ axis the volume contained between $y=c$ and $y=d$ is found from
$\displaystyle V= \int _ c^ d\pi (g(y))^2{\rm d}y =\int _ c^ d\pi x^2{\rm d}y$.
Integrals leading to logs
\[ \int \displaystyle \frac{f'(x)}{f(x)}\, {\rm d}x=\ln |f(x)| +c \]
Differential Equations
An equation that contains one or more derivatives is called a differential equation. $\displaystyle \frac{dy}{dx}=2y$ is called a first order differential equation as it involves a first order derivative $\displaystyle \frac{dy}{dx}$
Solving differential equations
A first-order differential equation that can be written as $\displaystyle \frac{dy}{dx}=f(x)g(y)$ may be solved by rearranging and integrating as
\[ \int \displaystyle \frac{1}{g(y)}\, dy = \int f(x)\, dx \]
Example:
\begin{eqnarray*} \displaystyle \frac{dy}{dx} & =& x^2y \\ \int \displaystyle \frac{1}{y}\, dy & =& \int x^2\, dx \\ \ln y & =& \displaystyle \frac{x^3}{3}+c \\ y & =& {\rm e}^{\frac{x^3}{3}+c} = A{\rm e}^{\frac{x^3}{3}} \end{eqnarray*}
where $A={\rm e}^ c$
This is called separating the variables.
