Coordinate Geometry
Linear Graphs and Equations
$y=mx+c$
$m$ = gradient, $c$ = vertical intercept.
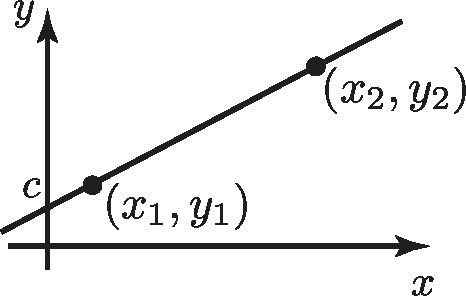
$ m=\displaystyle \frac{y_2-y_1}{x_2-x_1}$
Parallel lines have the same gradient.
Consider a line such as:
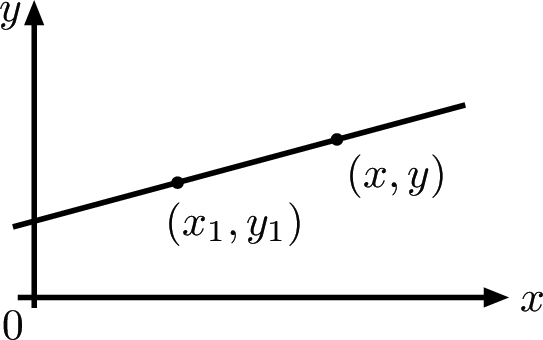
gradient $m = \displaystyle {y-y_1\over x-x_1}$
$\quad \quad \Rightarrow y-y_{1}= m(x-x_{1})$
This is another form for the equation of a straight line.
Yet another form is $ax + by + c = 0$
The mid-point of a straight line
The mid-point of a straight line connecting points $(x_{1},y_{1}) $ and $ (x_{2},y_{2})$.
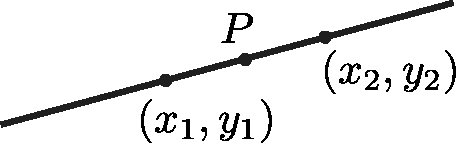
Mid point $P$ =$\biggl [\displaystyle \frac{x_{1}+x_{2}}{2},\displaystyle \frac{y_{1}+y_{2}}{2}\biggr ]$
The distance between two points
Take two points $(x_1, y_1)$ and $(x_2, y_2)$
distance = $\sqrt {(y_2-y_1)^2 + (x_2- x_1)^2}$
The equation of a circle
For a circle with centre $(0,0)$ and radius $r$:
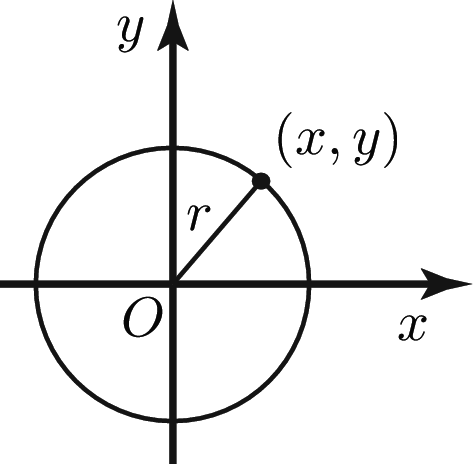
$x^2+y^2=r^2$
For a circle with centre $(a,b)$ and radius $r$:
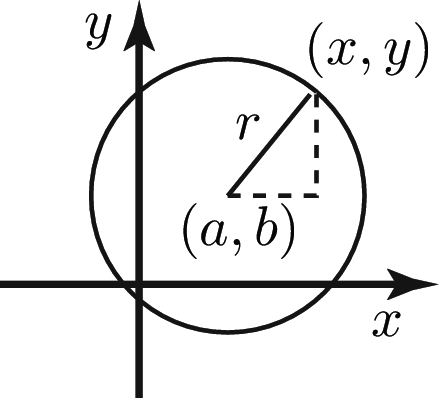
$(x-a)^2+(y-b)^2=r^2$
Tangent and normal to a circle
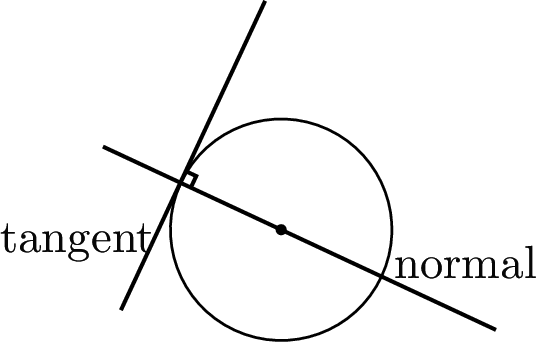
A tangent to a circle is a straight line that just touches it.
The normal to a circle is a straight line drawn at $90^\circ $ to the tangent at the point where the tangent touches the circle.
The normal always passes through the centre of the circle.
Gradients
If the gradient of the tangent is $m$, then the gradient of the normal is $\displaystyle \frac{-1}{m}$.
Gradient of normal $(m_{n}) = \displaystyle \frac{-1}{\hbox{gradient of tangent}(m_{t})}$
$\quad \quad \quad \quad \quad \quad \quad \Rightarrow m_{t} \times m_{n} = -1$
Parametric Equations
The coordinates of a point on a curve can be defined using parametric equations. With parametric equations $x$ and $y$ are expressed as $x=f(t)$ and $y=g(t)$ where the variable $t$ is called a parameter.
Examples of these parametric equations of curves are show below.
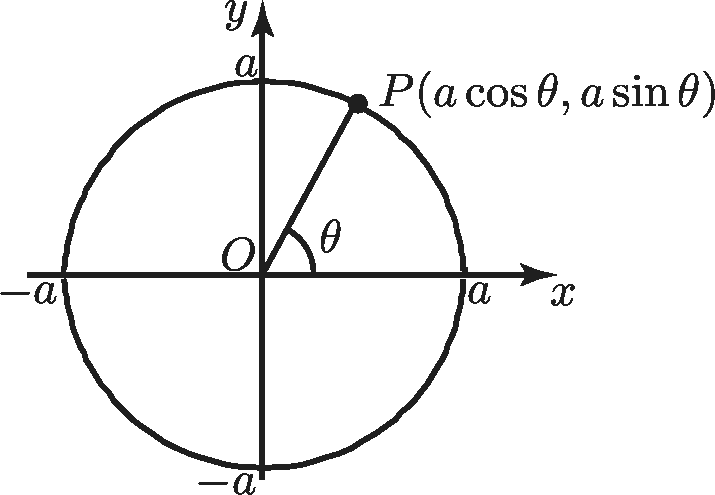
Circle
$x^2+y^2=a^2,\ x=a\cos \theta ,\ y=a\sin \theta $
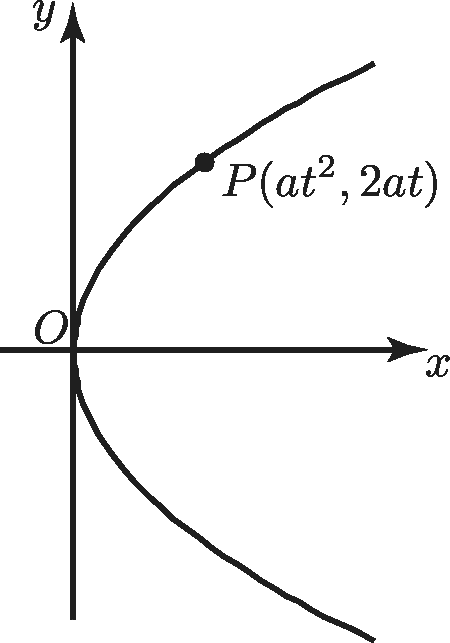
Parabola
$y^2=4ax,\ x=at^2,\ y=2at$
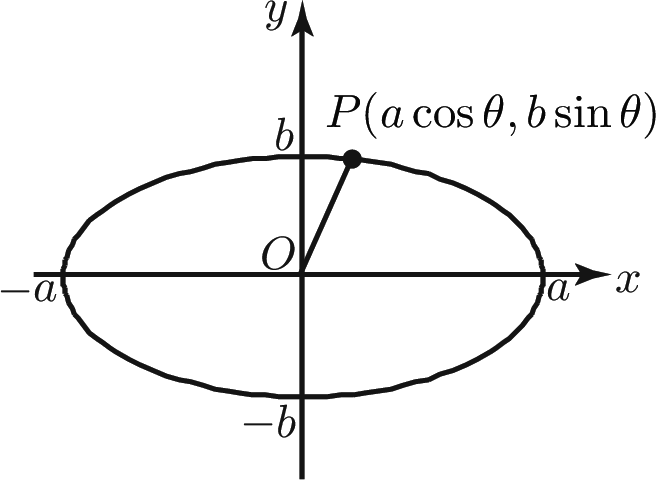
Ellipse
$\displaystyle \frac{x^2}{a^2}+\displaystyle \frac{y^2}{b^2}=1,\ x=a\cos \theta ,\ y=b\sin \theta $
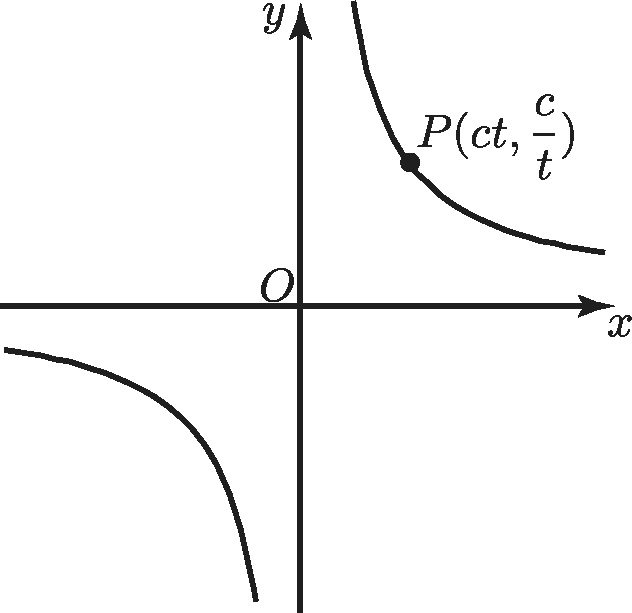
Rectangular hyperbola
$xy=c^2,\ x=ct,\ \displaystyle y=\frac{c}{t}$