Numerical Methods

Locating Roots of Equations

If you wish to solve an equation such as $x^3-3x^2-4=0$ a numerical method may be used to find the solutions.

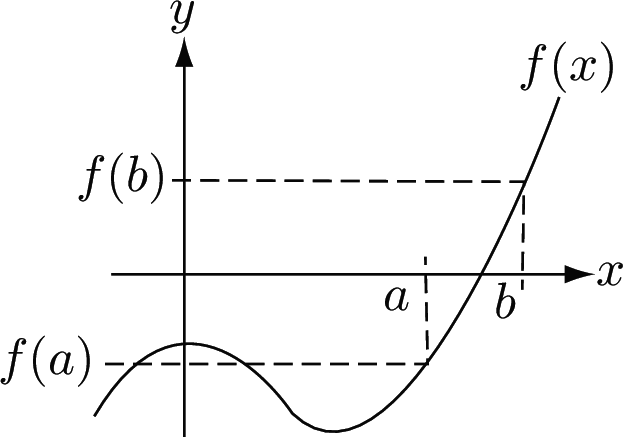
From the sketch $f(x)$ changes from negative to positive in the interval $a<x<b$. At least one root of the equation $f(x)=0$ must lie in this interval. For this example one root lies in the interval $3<x<4$.

Note:

• You can programme your calculator to make the solution easier.
• Different rearrangements of the equation $f(x)=0$ give iterative formulae that may lead to different roots of the equation, or may not even converge, so lead to no solution from a particular start location.

Iterative Methods for Solving Equations

An iterative formula has the form $x_{n+1} =g(x_ n )$. If such a formula converges to a limit, the value of the limit is the $x$ coordinate of the point of intersection of the graph of $y = x$ and $y = g(x)$.

Cobweb and Staircase Diagrams

It is sometimes possible to arrange an equation $f(x) = 0$ into the form $x_{n+1} = g(x_ n)$ and then to use this to find a solution of the original equation. This will depend upon whether the iteration converges. Diagrams can be drawn to determine convergence (or divergence). These are called cobweb and staircase diagrams.

Cobweb Diagram

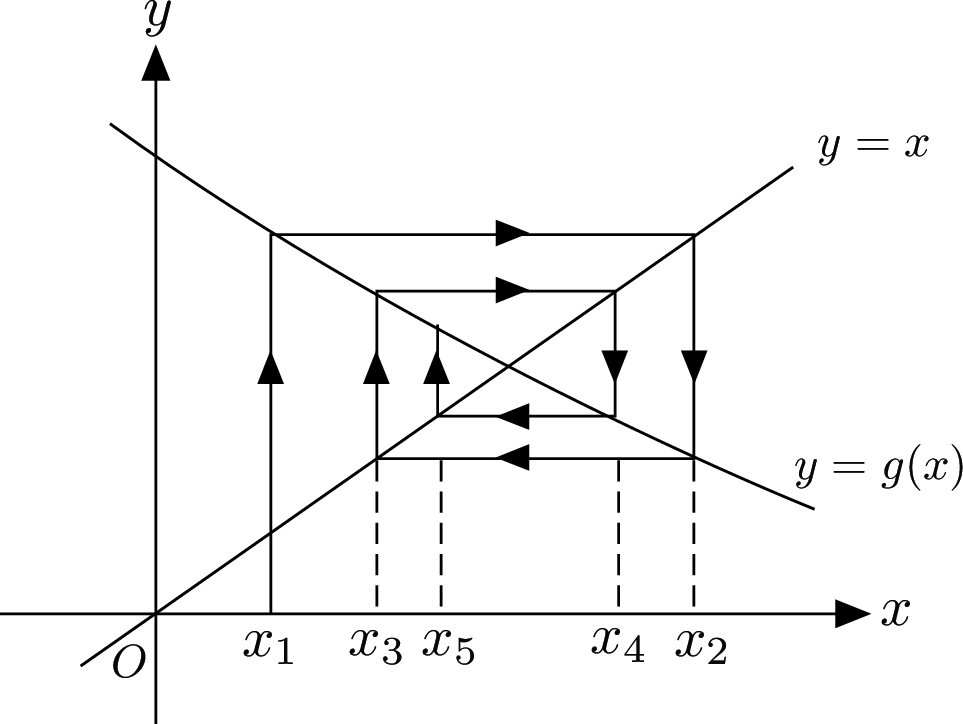
In this case the iteration is converging.

Staircase Diagram

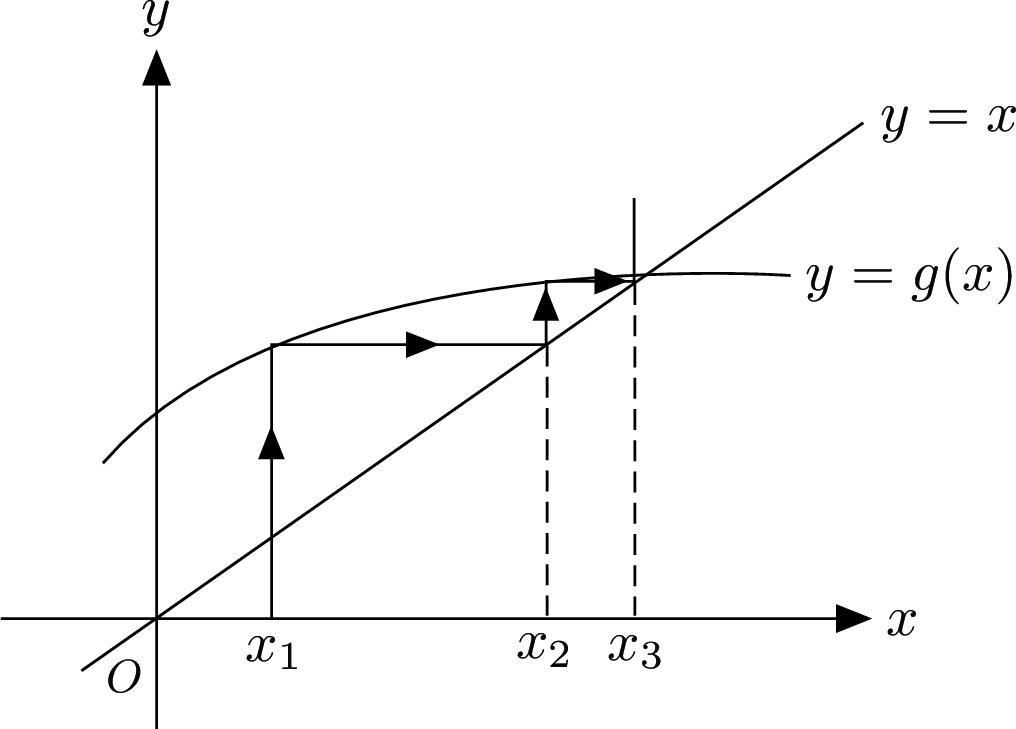
Again the iteration is converging.

If the iteration diverges then it is not appropriate to use it to obtain the solution.

For example:

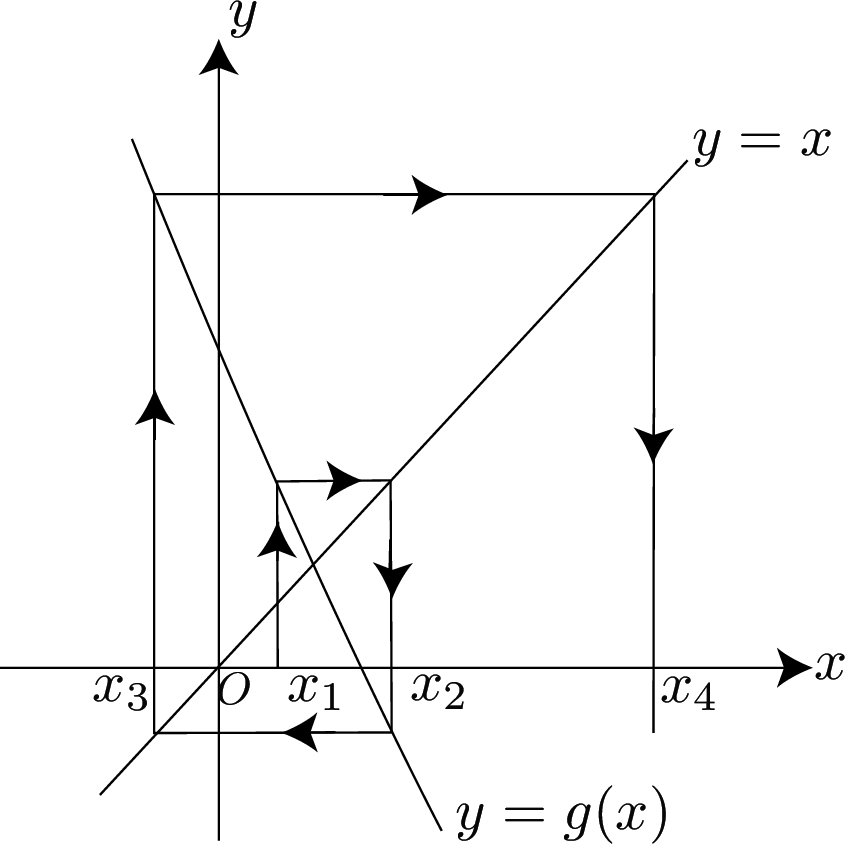
Newton Raphson Method

To solve $f(x) = 0$ use $x_{n+1} = x_ n - \displaystyle {f(x_ n)\over f’(x_ n)}$. This method is fast to converge, but convergence may not lead to the anticipated root.

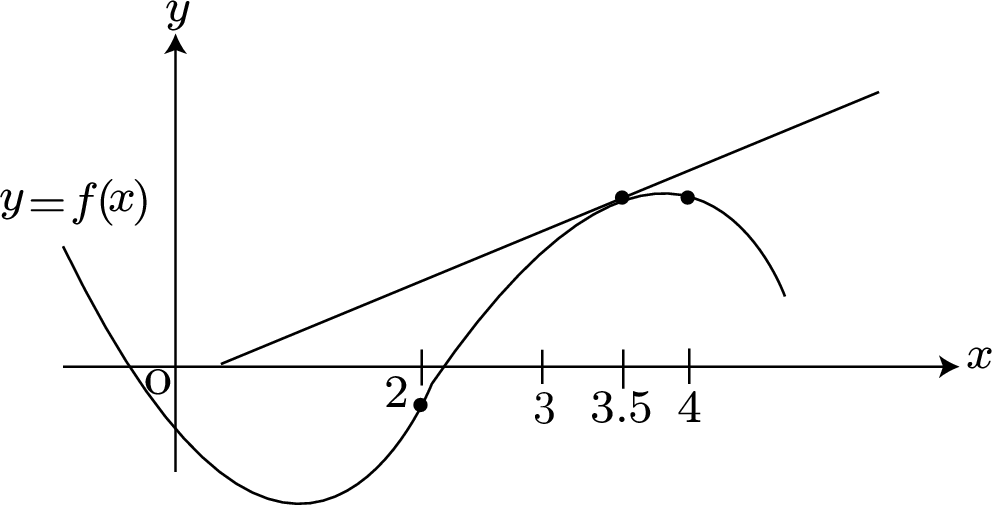
With an iteration starting at $x=3.5$ the sketch indicates likely convergence to a negative root instead of the anticipated root in $[2,3]$.

Numerical Integration

Not all functions can be integrated and, in this case, results can be found using numerical approximations. Three important methods are:

• the trapezium rule
• the mid-ordinate rule
• Simpson's rule

The Trapezium Rule

This rule is used to find the approximate area below a curve by dividing the region into a number of equal width strips, approximating these by trapezia, and calculating their total area.

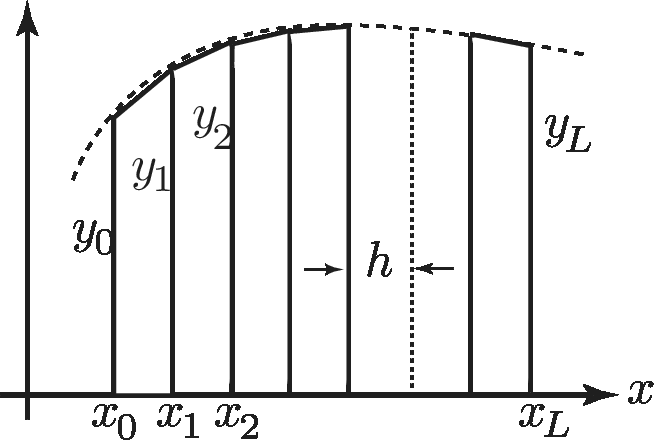
\[ A\approx {1\over 2} h\biggl \{ (y_0+y_ L) + 2(y_1+y_2+\ldots y_{L-1})\biggr \} \]

where $y_0$ and $y_ L$ are the first and last ordinates respectively and $h$ is the strip width.

The Mid-ordinate Rule

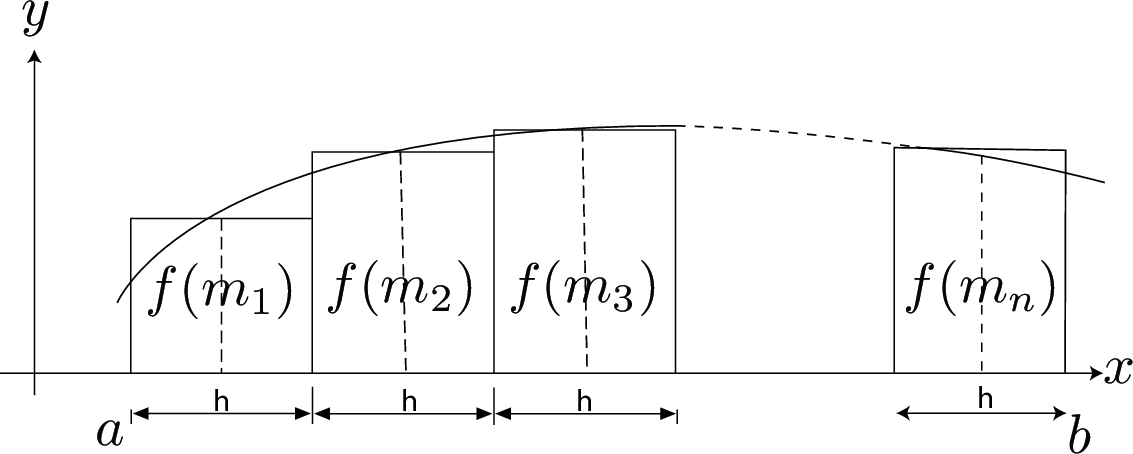
Width of strip $=\displaystyle \frac{b-a}{n}$ where $n$ is the number of strips.

\[ \int ^ b_ a f(x) dx \approx M_ n = h\biggl (f(m_1) + f(m_2) + \ldots f(m_ n)\biggr ) \]

where $m_1, m_2, m_3 \ldots m_ n$ are the values of $x$ at the midpoints of $n$ strips, each of width $h$.

$\hbox{Area } = \hbox{ width of strip } \times \hbox{ sum of the mid ordinates}$

Note – accuracy is improved with an increase in the number of strips.

Simpson's Rule

For most functions this will be more accurate than the mid-ordinate rule or the trapezium rule.

For Simpson's rule the region must be split into an even number of strips (and an odd number of ordinates).

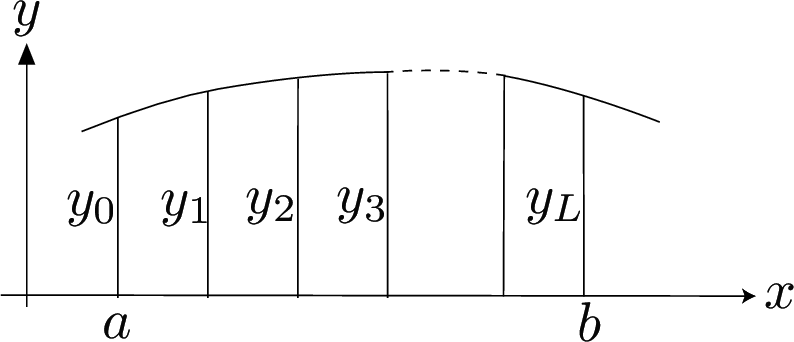
Simpson's rule says:

\[ \begin{array}{rcl} \displaystyle \int _ a^ b y(x) dx& \approx & {1\over 3}h \biggl [(y_0+y_ L) \biggr .\\ & +& 4(y_1+y_3+\ldots y_{L-1})\\ & +& \biggl .2(y_2+y_4+\ldots y_{L-2})\biggr ] \end{array} \]

Where $h=\displaystyle \frac{b-a}{n}$ and $n$ = number of strips.