Trigonometry
Degrees and radians
\[ 360^\circ = 2\pi \hbox{ radians},\quad 1^\circ ={2\pi \over 360}={\pi \over 180}\hbox{ radians} \]
\[ 1 \hbox{ radian} = {180\over \pi } \hbox{ degrees} \approx 57.3^\circ \]
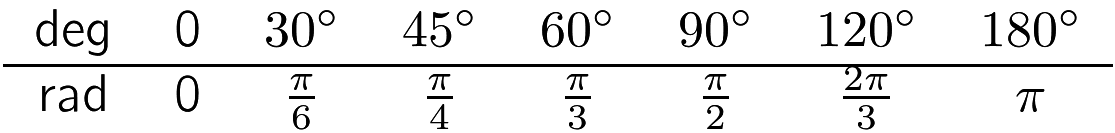
Pythagoras' Theorem
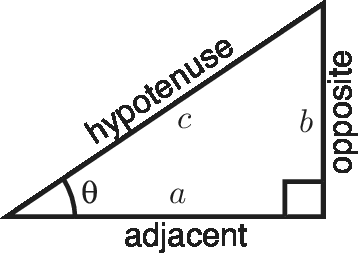
\[ a^2+b^2=c^2 \]
Trig ratios for an acute angle θ
$\displaystyle \sin \theta ={\hbox{side opposite to }\theta \over \hbox{hypotenuse}} ={ b\over c} $
$\displaystyle \cos \theta ={\hbox{side adjacent to }\theta \over \hbox{hypotenuse}} ={a\over c} $
$\displaystyle \tan \theta ={\hbox{side opposite to }\theta \over \hbox{side adjacent to }\theta } ={ b \over a} $
Standard triangles
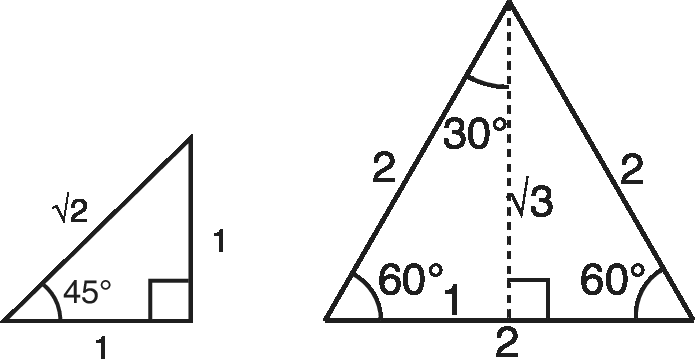
\[ \sin 45^\circ ={1\over \sqrt {2}} \qquad \cos 45^\circ = {1\over \sqrt {2}}\qquad \tan 45^\circ =1 \]
\[ \sin 30^\circ ={1\over 2} \qquad \cos 30^\circ ={\sqrt {3}\over 2}\qquad \tan 30^\circ ={1\over \sqrt {3}} \]
\[ \sin 60^\circ ={\sqrt {3}\over 2}\qquad \cos 60^\circ ={1\over 2}\qquad \tan 60^\circ ={ \sqrt {3}} \]
Trigonometric functions
Here, $x$ is an angle in degrees.
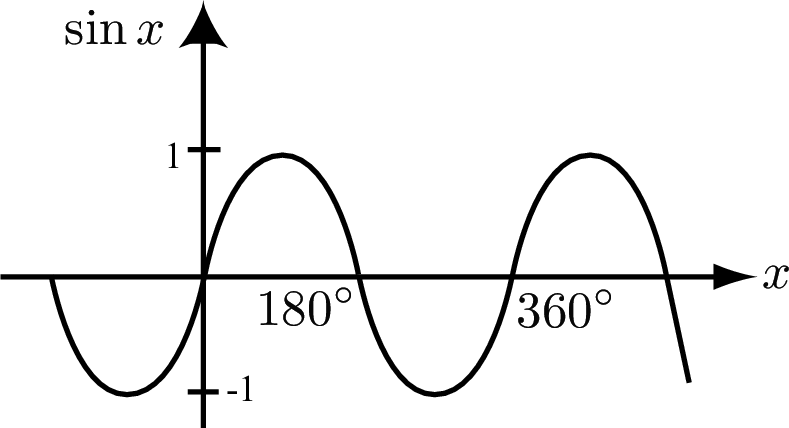
The sine and cosine functions are periodic with period $360^\circ $. The maximum value of these functions is 1. The minimum value is -1. We say that the amplitude is 1.
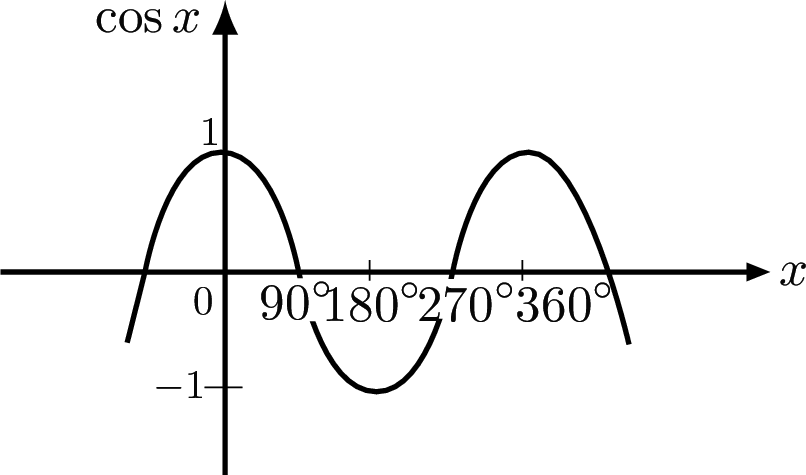
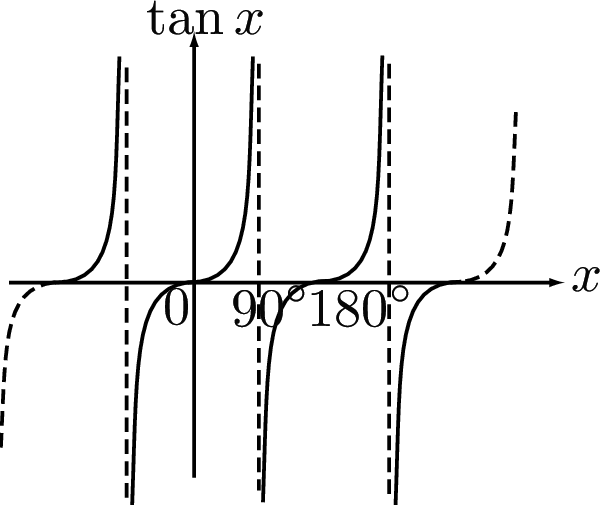
The tangent function is periodic with period $180^\circ $.
Key points about the graphs of trigonometric functions are:
$\sin (-\theta ) = -\sin \theta $
$\cos (-\theta ) =\cos \theta $
$\tan (-\theta ) = -\tan \theta $
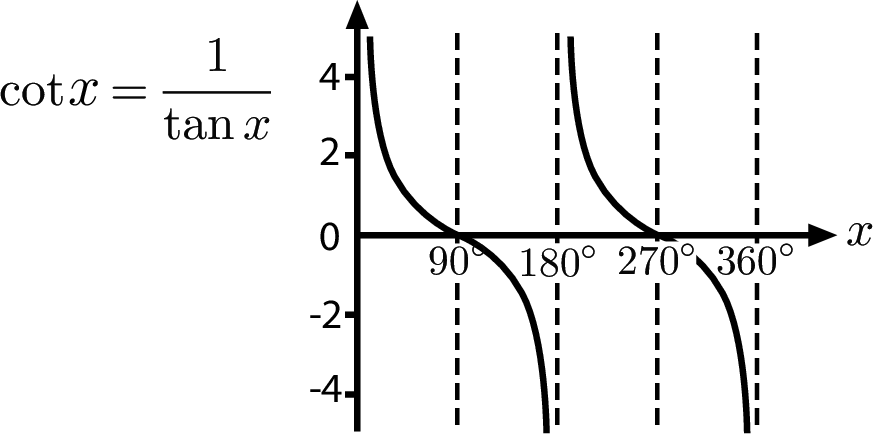
sec, cosec and cot
Here, $x$ is an angle in degrees.
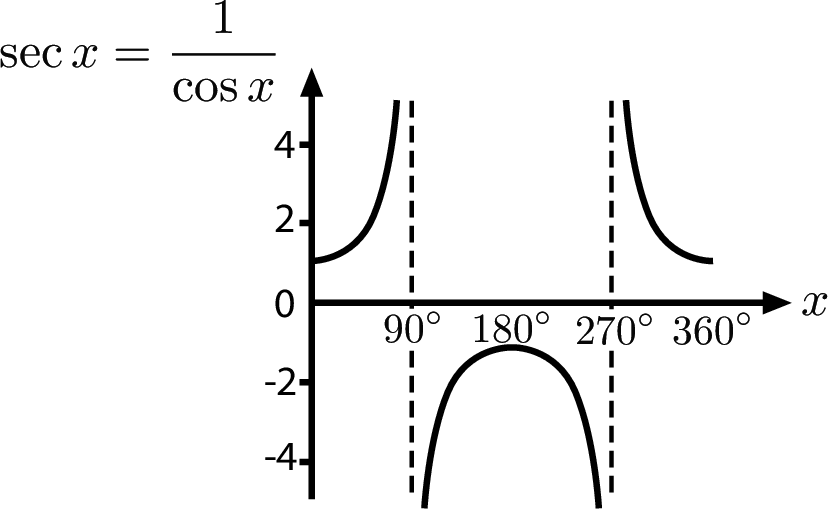
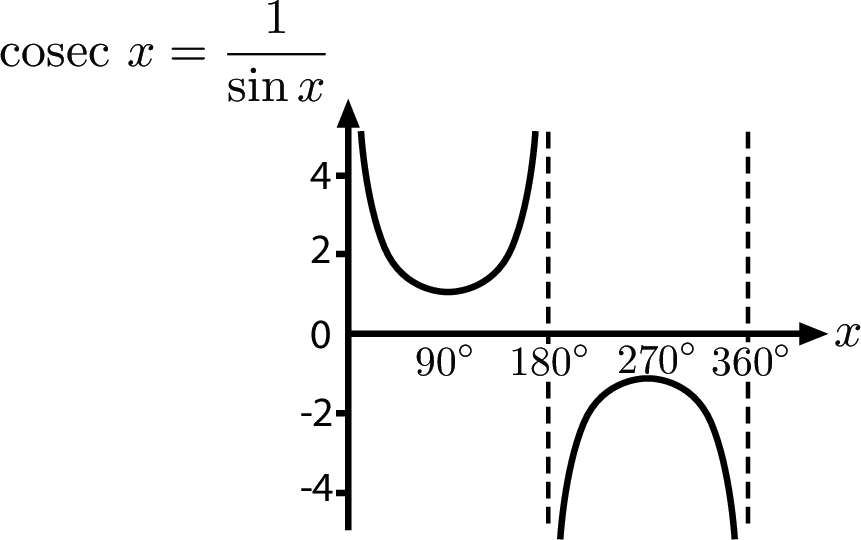
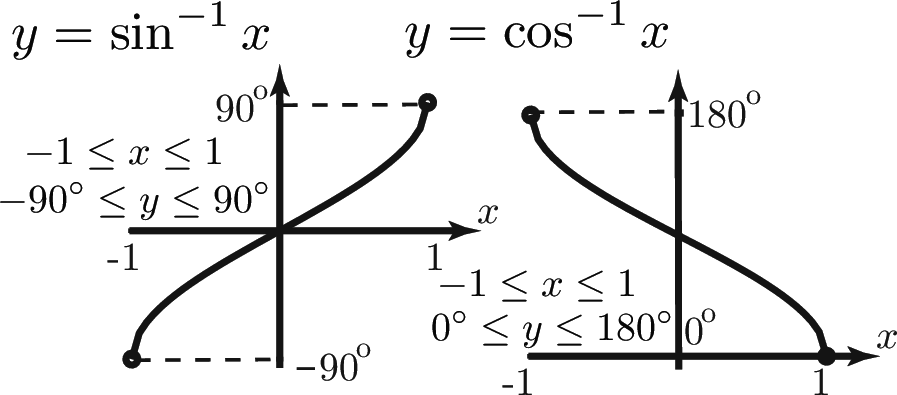
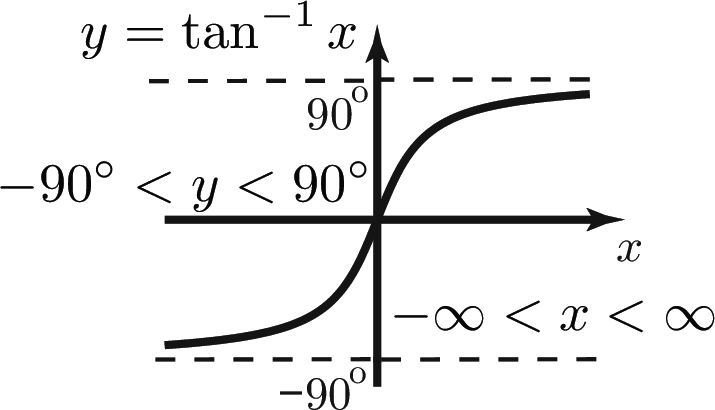
Graphs of Inverse Trigonometric Functions
$y=\sin ^{-1}x$, $y=\cos ^{-1}x$, and $y=\tan ^{-1}x$.
The inverse sine function, or arcsine, is denoted by $y=\sin ^{-1}x$. This means $y$ is the angle whose sine is $x$. Here, $x$ is a number such that $-1\le x\le 1$ , and $y$ is an angle in degrees. For example, $\sin 30^\circ = 0.5$ and so $30^\circ = \sin ^{-1}0.5$. There are analogous definitions of the inverse cosine function, $\cos ^{-1}x$ or $\arccos x$ and the inverse tangent function $\tan ^{-1}x$ or $\arctan x$.
Common Trigonometric Identities
\begin{eqnarray*} \tan \theta & =& \frac{\sin \theta }{\cos \theta }\\ \sec \theta & =& \frac{1}{\cos \theta }\\ \hbox{cosec}\, \theta & =& \frac{1}{\sin \theta }\\ \cot \theta =\frac{1}{\tan \theta }& =& \frac{\cos \theta }{\sin \theta }\\ \sin ^2\theta +\cos ^2\theta & =& 1\\ 1+\tan ^2\theta & =& \sec ^2\theta \\ 1+\cot ^2\theta & =& \hbox{cosec}^2\theta \\ \end{eqnarray*}
Addition Formulae
\[ \begin{array}{l} \sin (A+B)=\sin A\cos B+\cos A\sin B \\ \sin (A-B)=\sin A\cos B-\cos A\sin B \\ \cos (A+B)=\cos A\cos B-\sin A\sin B \\ \cos (A-B)=\cos A\cos B+\sin A\sin B \\ \tan (A+B)=\displaystyle \frac{\tan A+\tan B}{1-\tan A\tan B} \\ \tan (A-B)=\displaystyle \frac{\tan A-\tan B}{1+\tan A\tan B} \\ \end{array} \]
Double Angle Identities
\begin{eqnarray*} \sin 2A& =& 2\sin A\cos A \\ \cos 2A& =& \cos ^2A-\sin ^2A \\ & =& 2\cos ^2A-1 \\ & =& 1-2\sin ^2A \\ \tan 2A& =& \frac{2\tan A}{1-\tan ^2A}\\ \end{eqnarray*}
Products of Sines and/or Cosines
\[ \begin{array}{l} 2\sin A\cos B=\sin (A+B)+\sin (A-B) \\ 2\cos A\sin B=\sin (A+B)-\sin (A-B) \\ 2\cos A\cos B=\cos (A+B)+\cos (A-B) \\ 2\sin A\sin B=\cos (A-B) - \cos (A+B) \\ \end{array} \]
Sums or difference of Sines or Cosines
\[ \begin{array}{l} \sin A+\sin B=2\sin \left( {\frac{A+B}{2}} \right)\cos \left( {\frac{A-B}{2}} \right) \\ \sin A-\sin B=2\cos \left( {\frac{A+B}{2}} \right)\sin \left( {\frac{A-B}{2}} \right) \\ \cos A+\cos B=2\cos \left( {\frac{A+B}{2}} \right)\cos \left( {\frac{A-B}{2}} \right) \\ \cos A-\cos B=-2\sin \left( {\frac{A+B}{2}} \right)\sin \left( {\frac{A-B}{2}} \right) \\ \end{array} \]
Summing products of Sines or Cosines
For positive values of $a$ and $b$
$a\sin \theta +b\cos \theta =R\sin (\theta +\alpha )\ \ R>0,0^\circ <\alpha <90^\circ $ $a\sin \theta -b\cos \theta =R\sin (\theta -\alpha )\ \ R>0,0^\circ <\alpha <90^\circ $ $a\cos \theta +b\sin \theta =R\cos (\theta -\alpha )\ \ R>0,0^\circ <\alpha <90^\circ $ $a\cos \theta -b\sin \theta =R\cos (\theta +\alpha )\ \ R>0,0^\circ <\alpha <90^\circ $
Where $R=\sqrt {a^2+b^2} ,a=R\cos \alpha ,b=R\sin \alpha $
Small angles
For any small angle $\theta $, measured in radians
\[ \begin{array}{rcl} \sin \theta & \simeq & \theta \\ \tan \theta & \simeq & \theta \\ \cos \theta & \simeq & 1-{\theta ^2\over 2}. \end{array} \]
Triangles
The area
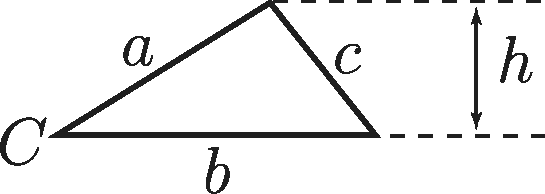
$\displaystyle A=\frac{1}{2}\times \hbox{base}\times \hbox{perpendicular height}=\frac{bh}{2}$
$\displaystyle A=\frac{1}{2}ab\sin C$
The sine and cosine rules
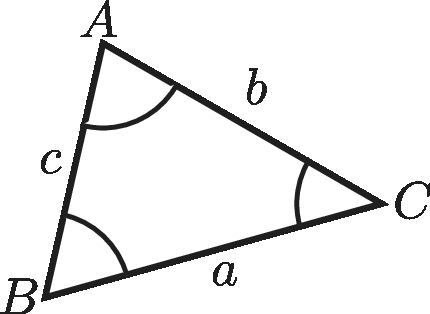
The sine rule: $\displaystyle {a\over \sin A}={b\over \sin B}={c\over \sin C} $
The cosine rule:
$ a^2=b^2+c^2-2bc\cos A $
Area of a sector
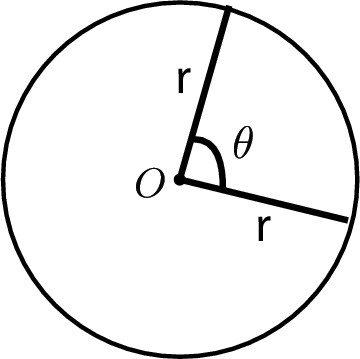
Area $= \frac{1}{2}r^2\theta $ where $\theta $ is in radians.
Arc Length
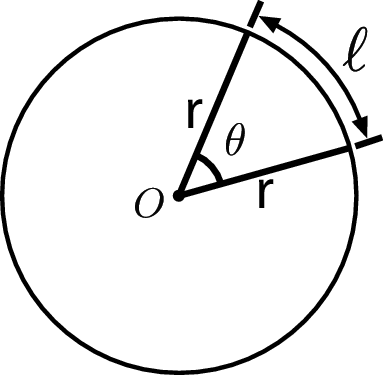
Arc length, $\ell = r\theta $ where $\theta $ is in radians.
