Vectors

• A vector is a quantity that has both magnitude and direction.
• Vectors that are equal have the same magnitude and direction.
• The magnitude of a vector is called its modulus.
• The modulus of a vector $\mathop a\limits _- $ is written as $|{\mathop a\limits _{-}} |$.
• The modulus of vector $\overrightarrow {AB} $ is written as $\left| {\overrightarrow {AB} } \right|$.
• The vector $-\mathop p\limits _- $ has the same magnitude as vector $\mathop p\limits _- $ but is in the opposite direction.
• A vector parallel to vector $\mathop a\limits _- $ can be written as $\lambda \mathop a\limits _- $ where $\lambda $ is a non zero scalar.
• A unit vector is a vector with modulus or magnitude 1.

Vectors in Two Dimensions

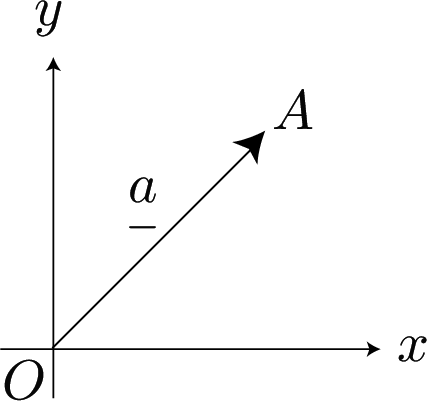
\begin{eqnarray*} {\rm Let}\ \overrightarrow {OA}& =& \mathop a\limits _- = \left({a_1\atop a_2}\right)\\ & =& a_1 \mathop i\limits _- +a_2 \mathop j\limits _-\quad \\ \end{eqnarray*}

where $\mathop i\limits _-$ and $\mathop j\limits _-$ are unit vectors in the $x$ and $y$ directions.

The modulus of $|\overrightarrow {OA}| = \sqrt {a^2_1+a^2_2}$

To find the vector

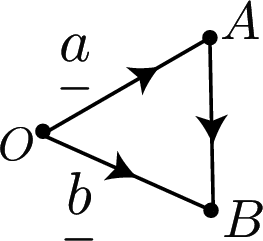
$\overrightarrow {AB} = {\mathop b\limits _- }-{\mathop a\limits _- }$

Vectors in Three Dimensions

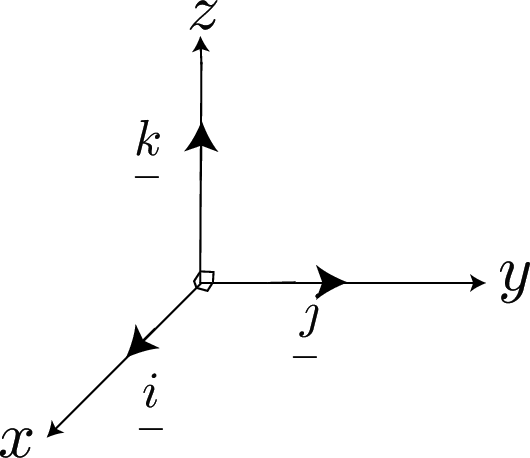
Here,

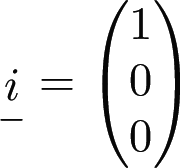
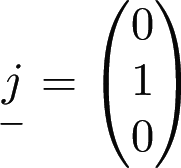
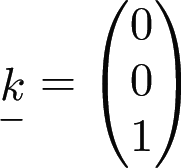
are unit vectors in the $x$, $y$ and $z$ directions.

In 3 dimensions the vector $\overrightarrow {OA}$ is given by

${\mathop a\limits _-} = a_1{\mathop i\limits _-} + a_2{\mathop j\limits _-} + a_3\mathop {\mathop k\limits _-} \hbox{ and } |\overrightarrow {OA}|=\sqrt {a_1^2+a_2^2+a_3^2}$

The Vector Equation of a Line in Two Dimensions

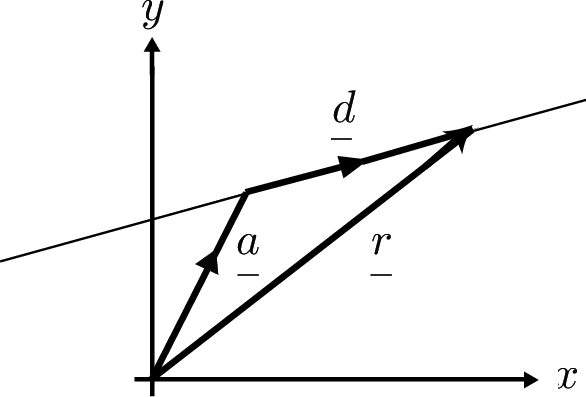
This is given as $\mathop r\limits _- =\left( {\begin{array}{l} x \\ y \\ \end{array}} \right)=\mathop a\limits _- +\lambda \mathop d\limits _- $

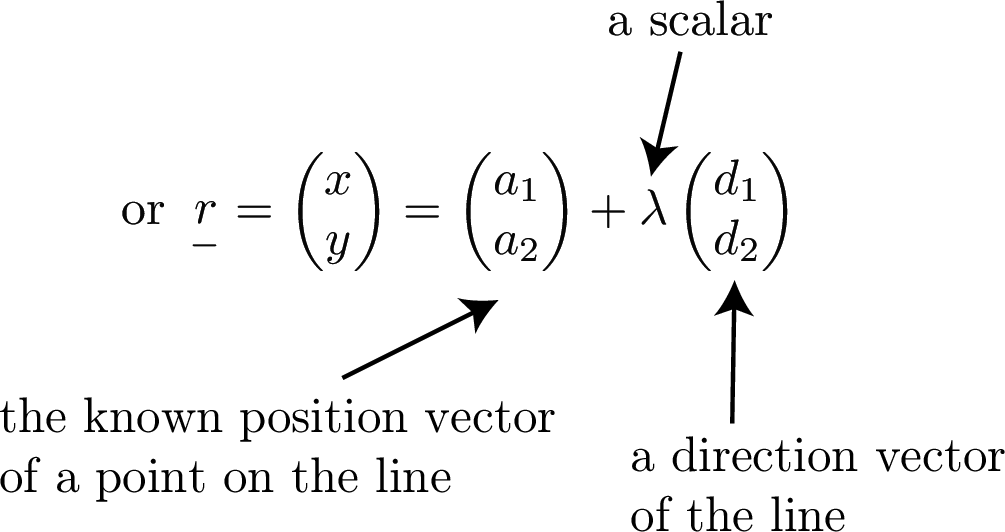
The Vector Equations of a Line in Three Dimensions

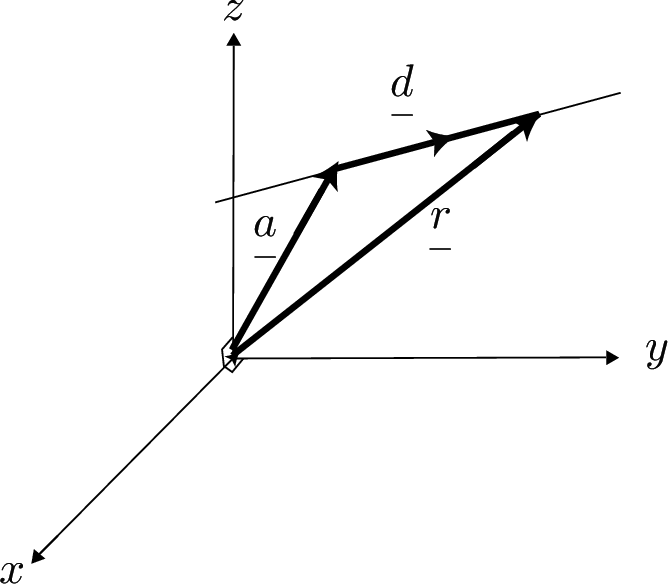
\[ \mathop r\limits _- = \left( {\begin{array}{l} x \\ y \\ z \\ \end{array}} \right)=\mathop a\limits _- +\lambda \mathop d\limits _- \]

Or $\mathop r\limits _- =\left( {\begin{array}{l} x \\ y \\ z \\ \end{array}} \right)=\left( {\begin{array}{l} a_1 \\ a_2 \\ a_3 \\ \end{array}} \right)+\lambda \left( {\begin{array}{l} d_1 \\ d_2 \\ d_3 \\ \end{array}} \right)$

The Scalar Product

For vectors $\mathop a\limits _- =\left( {\begin{array}{l} a_1 \\ a_2 \\ a_3 \\ \end{array}} \right)$ and $\mathop b\limits _- =\left( {\begin{array}{l} b_1 \\ b_2 \\ b_3 \\ \end{array}} \right)$ where $\theta $ is the angle between them

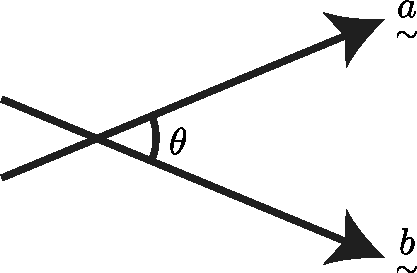
The scalar product is written as $\mathop a\limits _- .\mathop b\limits _- $ and is defined as $\mathop {a}\limits _- \cdot \mathop {b}\limits _- = |a|\cdot |b| \cos \theta $ where $\theta $ is the angle between the vectors. It follows that: $\begin{array}{l} \mathop a\limits _- .\mathop b\limits _- =\left( {\begin{array}{l} a_1 \\ a_2 \\ a_3 \\ \end{array}} \right).\left( {\begin{array}{l} b_1 \\ b_2 \\ b_3 \\ \end{array}} \right) \\ =a_1 b_1 +a_2 b_2 +a_3 b_3 \\ \end{array}$

Hence:

$\mathop a\limits _- .\mathop b\limits _- =a_1 b_1 +a_2 b_2 +a_3 b_3 =\left| {\mathop a\limits _- } \right|\left| {\mathop b\limits _- } \right|\cos \theta $

\[ \Rightarrow \cos \theta =\frac{a_1 b_1 +a_2 b_2 +a_3 b_3 }{\left| {\mathop a\limits _- } \right|\left| {\mathop b\limits _- } \right|} \]

If $\theta =90^\circ ,\cos \theta =0\Rightarrow \mathop a\limits _- \cdot \mathop b\limits _- =0$

For two vectors $\mathop a\limits _- $ and $\mathop b\limits _- $ to be perpendicular $\mathop a\limits _- .\mathop b\limits _- $= 0 assuming $\mathop a\limits _- $ and $\mathop b\limits _- $ are both non zero vectors.